W.M. van der Sande1*, A.D. Ashton2, P.C. Roos1, S.J.M.H. Hulscher1
1 University of Twente, This email address is being protected from spambots. You need JavaScript enabled to view it., This email address is being protected from spambots. You need JavaScript enabled to view it., This email address is being protected from spambots. You need JavaScript enabled to view it.
2 Woods Hole Oceanographic Institution, This email address is being protected from spambots. You need JavaScript enabled to view it.
Introduction
Coastlines are expected to retreat due to a globally accelerating sea-level rise. To anticipate future land loss, it is important to know how coastal zones will react to a rising sea, both now and on the long term. Here, we present a morphodynamic model that describes the transient development of a sandy wave-dominated shoreface. We then subject this model to sea-level rise to study how this affects the coast.
Methods
Our morphodynamic shoreface evolution model is based on descriptions of wave-induced sediment transport mechanisms, consisting of a slope-induced component directed offshore, and onshore-directed components resulting from shoaling of waves (Bowen, 1980). Assuming alongshore uniformity, these descriptions of sediment transport are coupled to bed development through the Exner equation (following Ortiz and Ashton, 2016). This results in a PDE bounded by the shoreline and a point (far enough) offshore. The onshore boundary is a moving boundary obeying a so-called Stefan condition as done by Swenson et al. (2005). Furthermore, a parametrized onshore overwash flux is added to the model formulation to represent back-barrier sediment deposition, which is widely recognized as the driving mechanism behind barrier beach persistence (Lorenzo-Trueba and Ashton, 2014).
Discretization of the model is done through a finite difference scheme; the Stefan condition is implemented through a fixed grid method that treats the shoreline boundary as an auxiliary variable. This numerical implementation results in short computation times (~10 minutes) for long simulation periods (~1000 years).
Results
Model simulations support earlier findings from Wolinsky and Murray (2009) by showing that the long-term retreat rate of the boundary depends on the regional slope and only initially follows the Bruun rule (Bruun, 1962). Over time, this results in faster retreating coast for shallow regional slopes (Figure 1) and slower retreating coasts for steep regional slopes (Figure 2) than predicted by the Bruun rule, although adjustments between short-term and long-term trajectories take significant (> 1000 yr) timescales to manifest, even for rapid rates of sea-level rise.
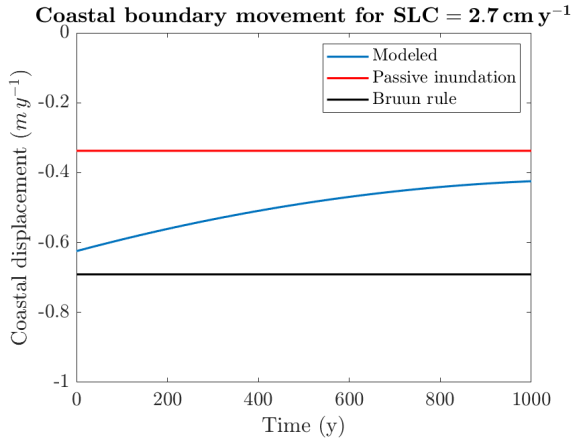
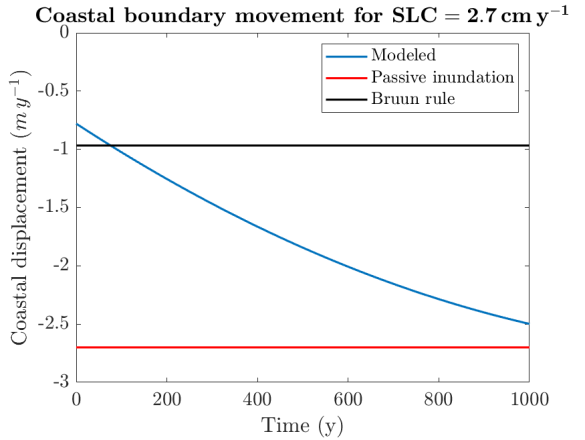
Figure 1: Boundary retreat rate for a shallow regional slope (0.01 m/m)
Figure 2: Boundary retreat rate for a steep regional slope (0.08 m/m)
References
Bowen, A.J., 1980. Simple models of nearshore sedimentation; beach profiles and longshore bars, in: McCann, S.B. (Ed.), The Coastline of Canada. Geological Survey Canada, pp. 1–11.
Bruun, P., 1962. Sea-Level Rise as a Cause of Shore Erosion. J. Waterw. Harb. Div. 88, 117–132.
Lorenzo-Trueba, J., Ashton, A.D., 2014. Rollover, drowning, and discontinuous retreat: Distinct modes of barrier response to sea-level rise arising from a simple morphodynamic model. J. Geophys. Res. Earth Surf. 119, 779–801. doi:10.1002/2013JF002941.Received
Ortiz, A.C., Ashton, A.D., 2016. Exploring shoreface dynamics and a mechanistic explanation for a morphodynamic depth of closure. J. Geophys. Res. Earth Surf. 121, 442–464. https://doi.org/10.1002/2015JF003699.Received
Swenson, J.B., Paola, C., Pratson, L., Voller, V.R., Murray, A.B., 2005. Fluvial and marine controls on combined subaerial and subaqueous delta progradation: Morphodynamic modeling of compound-clinoform development. J. Geophys. Res. Earth Surf. 110, 1–16. https://doi.org/10.1029/2004JF000265
Wolinsky, M.A., Murray, A.B., 2009. A unifying framework for shoreline migration: 2 . Application to wave-dominated coasts. J. Geophys. Res. 114, 1–13. https://doi.org/10.1029/2007JF000856
