M.P. Rozendaal1*, Y.M. Dijkstra1, H.M. Schuttelaars1,
1 Delft Institute of Applied Mathematics, Delft University of Technology;
*corresponding author: This email address is being protected from spambots. You need JavaScript enabled to view it.
Introduction
Estuaries are important features that can be found all around the world. Accurately estimating the water level in such systems is of crucial importance. However, the highly dynamical nature of estuaries makes modelling the water motion particularly challenging. Even though the increase in computational power allows the use of complex 3D models to analyse this water motion, depth-averaged 2DH models are often used. The reason for this is twofold: firstly, they are much faster than their 3D counterparts and secondly, the results obtained with a 2DH model are considered adequate for many applications.
This implicitly assumes that the depth-averaged results from a 3D model and those obtained using a 2DH model are the same. Even though some efforts have been made to compare both 3D and 2DH results to measurements (Marinone, 2000), no systematic analysis is presented in the literature, not even for the linearized tidal dynamics. Focusing on the linearized dynamics, the main aim of this contribution is to investigate if it is possible to consistently parameterise 3D effects in a 2DH model such that both models describe the same depth-averaged dynamics, e.g., resonance, transport and water levels, and (if possible) to derive this parametrisation.
Methods
As a first step we restrict ourselves to the linearized water motion. To obtain an exact reduction from a linearized 3D model to a 2DH model an analytical approach is necessary. We start with the linearized three-dimensional shallow water equations, see e.g. Kumar (2018). For the water motion consisting of a single tidal constituent, i.e., a harmonic signal, the vertical structure can be obtained analytically, see Winant (2007). Using this analytical vertical solution we are able to derive an exact closure relationship between the velocity at the bed and the depth-averaged velocity, resulting in an exact reconstruction of depth-averaged 3D results in a 2DH model. In addition, using advanced mathematical techniques, we are able to extend this result to non-harmonic models, i.e., models solving the tidal dynamics using time-stepping techniques.
Results
The exact reduction culminates into a new friction formulation for both harmonic and non-harmonic 2DH models that parameterises the effect of 3D dynamics. That is, given the 3D parameters, an exact parameterisation for the 2DH parameters is found such that their depth-averaged dynamics are the same. For harmonic models, the three most striking features of this new friction formulation are that the friction coefficient has an amplitude that depends in a complex way on the local water depth and tidal frequency, a phase (shift) relative to the depth-averaged velocity and that it depends on both depth-averaged velocity components. For non-harmonic models, it additionally shows that the friction felt by the system depends not only on the instantaneous velocity but also on the velocities in the past. During the presentation, we illustrate the effects of using this friction formulation on the water motion in a typical estuary by comparing it with results obtained using more commonly applied friction formulations.
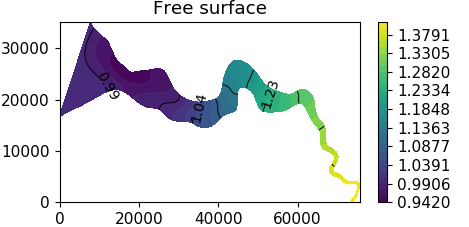
Figure 1: The absolute value of the free surface of the M2 tidal constituent in the Scheldt estuary.
References
Marinone, S. G. (2000). Tidal currents in the Gulf of California: Intercomparisons among two-and three-dimensional models with observations. Ciencias Marinas, 26(2), 275-301. https://doi.org/10.7773/cm.v26i2.579
Kumar, M. (2018). Three-dimensional model for estuarine turbidity maxima in tidally dominated estuaries. PhD thesis, Delft University of Technology.
Winant, C. D. (2007). Three-dimensional tidal flow in an elongated, rotating basin. Journal of Physical Oceanography, 37(9), 2345-2362. https://doi.org/10.1175/JPO3122.1
