Dano Roelvink,1,2,3, Bas Huisman2 and Johan Reyns1,2,3
1 IHE Delft Institute for Water Education; 2 Deltares; 3 Delft University of Technology
*corresponding author: This email address is being protected from spambots. You need JavaScript enabled to view it.
Introduction
The effect of tides on the total, tide-averaged longshore transport can be profound but is not easy to represent in existing bulk transport formulas. The formula by van Rijn (2014) allows for the inclusion of a tidal velocity, but this leaves open the question of how this is varying in space, across the profile and through the tidal cycle. In the framework of the ShorelineS TKI project, a collaboration between 15 companies and institutes to operationalize the ShorelineS model (Roelvink et al, 2020) for coastal engineering applications, including the effects of tides featured prominently. Here we outline a method, inspired by that by Southgate (1989), to accurately deal with the combination of vertical and horizontal tides and obliquely incident waves to predict longshore transport rates.
Methods
The longshore velocity due to tidal water level gradients can be solved analytically using linearized bottom friction. The solution includes the effect of inertia and describes the amplitude and phase of the longshore velocity as a function of the amplitude and phase of the water level and the mean water depth. We can apply this, e.g., to the M2 and M4 components, and obtain estimates of the tidal velocity signal; a residual component can be resolved as well. Wave-driven currents through the tidal cycle can be computed by solving the wave direction and cross-shore wave energy balance for each tidal water level, and solving the longshore velocity from the balance between longshore forcing and bed friction. The resulting tidal velocity and wave-driven current, both functions of cross-shore distance and tidal phase, can be fed into a transport formulation such as Soulsby-van Rijn, integrated over the nearshore zone and averaged over the tidal cycle. This principle was implemented in a highly efficient Matlab function that can be called from within the ShorelineS model just like other bulk transport formulas. The tidal coefficients needed can be easily extracted from a series of observations along a depth contour in a 2D tidal model.
Results
The method of reproducing tidal velocity time series was tested using data from a Delft3D model of the coast of Flanders and the Netherlands. A typical time series 14km east of Zeebrugge and the longshore distribution of the tidal velocity skewness, a proxy for tidal transport, is shown in Figure 1; the analytical model accurately reproduces the tidal features. More comparisons and an application in ShorelineS will be presented at the NCK days.
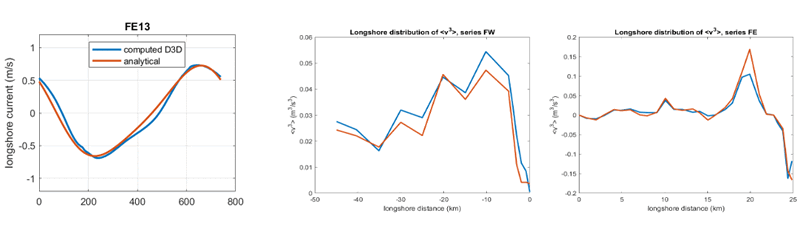
Figure 1: Example time series of tidal velocity (left panel); longshore distribution of tidal velocity skewness, West (middle) and East (right panel) of Zeebrugge
References
Van Rijn, L.C (2014). A simple general expression for longshore transport of sand, gravel and shingle. Coastal Engineering 90, 23-39.
D Roelvink, B Huisman, A Elghandour, M Ghonim, J Reyns (2020). Efficient modeling of complex sandy coastal evolution at monthly to century time scales. Frontiers in Marine Science 7, 535.
Southgate, H.N. (1989). A nearshore profile model of wave and tidal current interaction. Coastal Engineering, 13 (1989) 219-245.
