L. Portos-Amill*, P.C. Roos, J.H. Damveld, S.J.M.H. Hulscher
Water Engineering and Management, University of Twente, The Netherlands
*corresponding author: This email address is being protected from spambots. You need JavaScript enabled to view it.
Introduction
The effects of bedforms (tidal sand waves as well as sand banks) are usually not considered in hydrodynamic basin-scale modeling studies (see Brakenhoff et al., 2020, and references therein). Instead, the friction coefficient is taken as a calibration parameter, moreover it is taken constant in the entire domain. We derive a physics-based mathematical formulation to parametrize the bed shear stress experienced by the flow over a bedform field in a basin-scale domain (such as the North Sea).
Methods
The depth-averaged, shallow water equations on the f-plane are spatially averaged over bedform field scales. For convenience, as a first step, we consider the local bed shear stress (τb) to depend on the linear friction coefficient r, τb,x = ru, τb,y = rv, where u and v are the depth-averaged components of the flow. The resulting parametrizations include information on the local bedform characteristics, such as shape, height and orientation. Thus, a basin-scale model using such parametrizations could solve the hydrodynamics without resolving each bedform, but still account for their effects.
Results
We have computed the effective friction (that containing the effects of bedforms) for two different bedform profiles (one purely sinusoidal, and the other more sharply crested, see Figure 1). Results show that the friction coefficient increases with increasing bedform height. Furthermore, the friction depends on the bedform shape, as well as on the orientation with respect to the flow (the latter not being shown here).
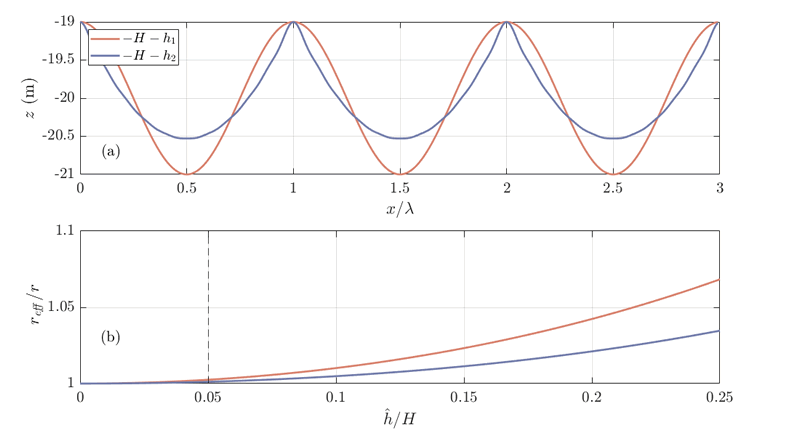
Figure 1: (a) Different sand wave profiles used in the present study, and (b) resulting effective friction coefficient reff relative to the reference friction r for different sand wave field amplitudes (ĥ) to mean water depth (H) ratio. The vertical dashed line in panel (b) corresponds to the situation depicted in panel (a), where the sand wave field amplitude is 1 m, and mean water depth H = 20 m. We have taken the Coriolis parameter representative of the North Sea (f = 1.15·10-4 s-1), and a linear friction coefficient r = 2.5·10-3 m/s.
References
Brakenhoff et al. (2020). Journal of Marine Science and Engineering, 8(11), 892.
