P.C. Roos1*, H.M. Schuttelaars2
1 University of Twente; 2 Delft University of Technology
*corresponding author: This email address is being protected from spambots. You need JavaScript enabled to view it.
Introduction
The extent to which the inlets in a mesotidal barrier coast, e.g. the Wadden Sea, morphodynamically influence one another is of both theoretical and practical interest. For example, dredging operations in one inlet may lead to sedimentation at another inlet. Based on Escoffier's (1940) principle, past studies have focused on the cross-sectional stability of an inlet system, i.e. whether the system returns to equilibrium after perturbing one or more inlets (e.g., Roos et al. 2013). However, inlet stability does not address the extent to which inlets influence each other morphodynamically, a new concept which we shall refer to as inlet connectivity. Inlet connectivity is likely to depend on various characteristics such as basin geometry, inlet spacing and tidal divides. The goal of this study is twofold: (i) to introduce and quantify this new concept of inlet connectivity, and (ii) to implement and analyse it in an exploratory double inlet model, that includes a tidal divide (Fig.1a).
Methods
Starting from a stable equilibrium in a multiple inlet system, consider the system's return to equilibrium after perturbing one of the inlets, while leaving the other(s) unaffected. The connectivity quotient Cjq measures the maximum cross-sectional change experienced by the (initially unperturbed) inlet j, divided by the initial perturbation of inlet q's cross-section (Fig.1b). Large values of |Cjq| suggest strong connectivity, whereas Cjq≈0 implies weak connectivity. We then implement this in a new double inlet model, based on Roos et al. (2013), that includes tidal divides using a stepped topography (Fig.1a).
Results
Model results demonstrate how increasing the tidal divide's height or width either may turn an unstable inlet system into a stable one, or reduces connectivity if it is already stable (Fig.1c). All our simulations reveal negative values of the connectivity quotient: the system's return to equilibrium after an increase (decrease) in the cross-section of inlet 1 is attended with a decrease (increase) in inlet 2, and vice versa. Further model results will be presented and the implications for the Western Wadden Sea (Texel inlet, Vlie inlet and Eijerlandse Gat system) will be discussed.
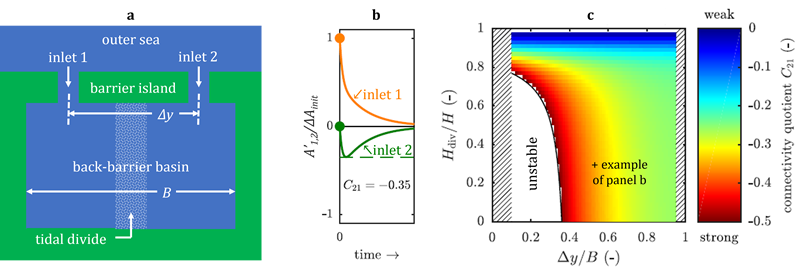
Figure 1: (a) Top view of model geometry showing double inlet system with tidal divide. (b) Example of system's return to equilibrium after perturbing inlet 1, corresponding to a connectivity quotient of C-21=-0.35. The plot shows the time evolution of the perturbations to inlet 1 (A'1 in orange) and 2 (A'2 in green), scaled with inlet 1's initial perturbation ∆Ainit. (c) Sensitivity of connectivity quotient to inlet spacing ∆y and tidal divide height Hdiv (scaled with basin width B and depth H, resp.). The example shown in panel b is denoted with +. Red (blue) shades indicate strong (weak) connectivity.
References
Escoffier, F.F. (1940). The stability of tidal inlets. Shore and Beach, 8, 114–115.
Roos, P.C., Schuttelaars, H.M., & Brouwer, R.L. (2013). Observations of barrier island length explained using an exploratory morphodynamic model. Geophys. Res. Lett., 40(16), 4338–4343.
