Karl Kästnera, A.J.F. Hoitinka, P. J. J. F. Torfsa, E. Deleersnijderb,c, N. S. Ningsihd
aHydrology and Water Management, Wageningen University
bInstitute of Mechanics, Materials and Civil Engineering, Université catholique de Louvain, Belgium
cDelft Institute of Applied Mathematics, Technical University Delft, Delft, The Netherlands
dResearch Group of Oceanography, Bandung Institute of Technology, Bandung, Indonesia
Keywords: tides, river delta, river discharge, bed slope
Tidal rivers are conceptualized as narrow channels along which the cross-section geometry remains constant and the bed is horizontal. As the tide propagates upriver, it is damped by friction and the amplitude decreases exponentially (Figure 1d, dashed) (Friedrichs, 2010). The strength of the damping increases with the river flow (Godin, 1991). At the river mouth, the tidally averaged water level changes little throughout the year. However, further upstream, the water depth seasonally varies with the river discharge. Our observations from the Kapuas River, Indonesia (Figure 1a), show that the water surface forms a backwater profile when the river flow is low, so that the depth gradually decreases into the upstream direction (Figure 1b). This influences how the tide propagates so that the amplitude does not decrease exponentially anymore (Figure 1c). We analyze this phenomenon theoretically and reveal several so far overlooked aspects of river tides, which are particularly relevant for low river flow (Figure 1d, solid). In the downstream part of the tidal river, depth- convergence compensates frictional damping so that the tidal range is higher than expected. Farther upstream, frictional damping is strong due to the shallow depth. This rapidly attenuates the tide. The tide effectively does not propagate beyond the point where the bed reaches sea level. This also applies to the overtide and the subtidal water level setup.
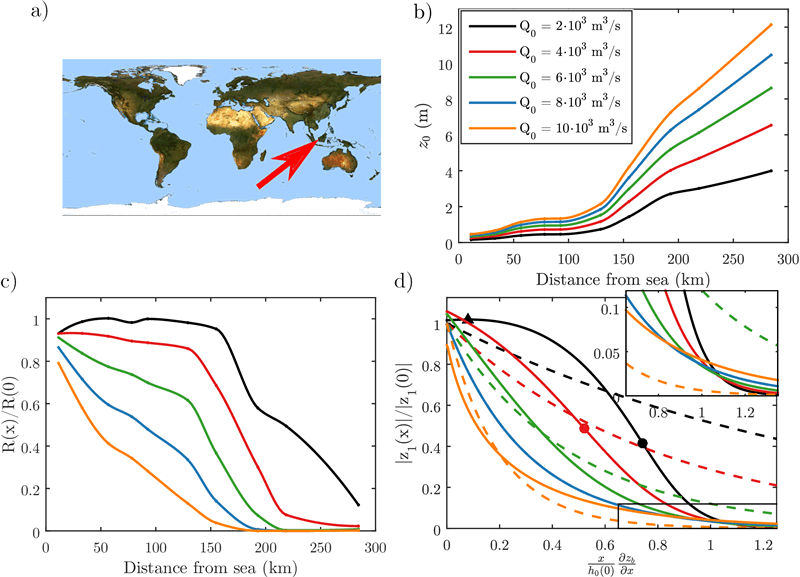
Figure 1: Location of the Kapuas Delta in Indonesia (a), Observed tidally averaged water level (b) and tidal admittance (c) along the Kapuas River, tidal admittance as predicted with a conventional model that ignores the bed slope (d, dashed) and by the extended model that incorporates backwater effects (d, solid)
References
Friedrichs, C.T., 2010. Barotropic tides in channelized estuaries, in: Valle-Levinson, A. (Ed.), Contemporary Issues in Estuarine Physics. Cambridge University Press, Cambridge, pp. 27–61.
Godin, G., 1991. Frictional effects in river tides, in: Tidal Hydrodynamics. John Wiley & Sons. volume 379, p. 402.
Kästner, K., Hoitink, A.J.F., 2019. Effects of a sloping bed on the propagation of tides up-river. Submitted to J. of Fluid Mechanics
