A.P. Iwantoro1*, M. van der Vegt1, M.G. Kleinhans1
1 Utrecht University, This email address is being protected from spambots. You need JavaScript enabled to view it., This email address is being protected from spambots. You need JavaScript enabled to view it., This email address is being protected from spambots. You need JavaScript enabled to view it.
Introduction
The morphology of river bifurcations often evolves asymmetrically, resulting in an avulsion (i.e. unstable bifurcations). Observations suggest that bifurcations in tidally influenced systems are stable. Here we study the morphological evolution of bifurcations in the range from river- to tide-dominated systems.
Methods
We developed a 1D numerical model that solves the 1D shallow water equations, sediment transport and the sediment mass conservation equation for a system consisting of one upstream channel and two downstream branches. The sediment division at the bifurcation includes both bed-load and suspended load transport and can cover the changing flow directions in tidal systems. The division of bed-load at the junction was affected by both cross-channel flow and transverse bed slopes, while for suspended load, it is only affected by cross-channel flow.
To analyse the stability of the bifurcations, identical branches were initially defined. Then a small depth difference between branches was prescribed. When this depth asymmetry grows in time the system is unstable, when it decays it is stable. The channel configuration and other model settings were based on observed bifurcations. In shown results, the Shields number was varied by varying the D50 in the range of sandy material (0.1-1 mm) and the width-to-depth ratio was varied in the range between 10 and 50 by varying the width while keeping the same discharge per unit width.
Results
Based on four sets of simulations with different tidal influence (Fig. 1), we conclude that tides cause a wider range of condition for which stable bifurcations can occur. From these results, we proof that tides can counteract the avulsion process that would occur in river-dominated deltas. Using this new model, we can start analyzing how different combinations of tide and river forcing determine the morphological stability of bifurcations, and how this depends on the geometry of the bifurcation.
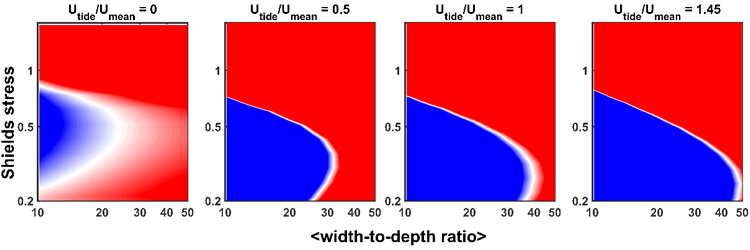
Figure 1 Stability of bifurcations for fluvial influenced (Utide/U0 at the bifurcation = 0) and fluvial-tidal influenced cases with channel slope = 3e-5. Red and blue indicates unstable and stable condition, respectively. Utide and Umean are tide-induced and tidally averaged flow magnitudes at the junction, respectively.
